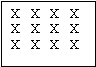
III INCONTRO
Le maestre illustrano il percorso didattico utilizzato per l’apprendimento delle operazioni, si discute sulle ipotesi di introduzione di moltiplicazione e divisione nelle prime classi.
La prof. Longo chiede che vengano esplicitate con esempi le modalità di presentazione nelle classi.
Si inizia esemplificando l’introduzione della moltiplicazione in una seconda elementare.
Il suggerimento è ancora di partire dai problemi.
Una maestra illustra l’esempio adottato recentemente in classe:
In casa ho tre tipi di pasta e 4 di sugo, quanti primi piatti diversi posso preparare?
|
|
Pesto |
Ragù |
Burro |
Pomodoro |
|
Maccheroni |
... |
... |
... |
... |
|
Farfalle |
... |
... |
... |
... |
|
Spaghetti |
... |
... |
... |
... |
Non si dice ancora agli allievi che questa è una moltiplicazione.
Dalla tabella si può passare ad uno schema fatto con un simbolo, sostituendo ad es. delle crocette:
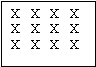
![]()
![]()
Ogni X indica una coppia e il bambino conta i 12 simboli.
La simbolizzazione dovrebbe nascere dagli alunni come esigenza per rappresentare più agevolmente la situazione. L’insegnante deve guidarli in questo percorso.
Vengono proposte anche simbolizzazioni diverse nei problemi, ad es.:
|
pesto |
||
|
burro |
|
pomodoro |
|
ragù |
Per arrivare ad una simbolizzazione unica può essere positivo avere uno scopo: la simbolizzazione deve essere sintetica e univoca per comprendersi.
Si mettono poi in evidenza alcune scritte che generano confusione :
3 X 4 e 3 + 4
se il bambino le confonde è perché non ne ha ancora compreso il loro significato.In tal caso lo si deve far ragionare sul significato del simbolo, il solo apprendimento meccanico non è duraturo, occorre la piena comprensione cioè collegare il simbolo con le azioni.
La prof. Longo mette in evidenza come le proprietà delle operazioni adeguatamente introdotte, costituiscano un mezzo importante per far riflettere sulle operazioni e comprenderle meglio.
Come es. ci si chiede se vale sempre la proprietà commutativa della moltiplicazione nei problemi.
Ho tre pulcini, quante zampe in tutto ?
E’ un problema di corrispondenza
|
Pulcini |
Zampe |
|
1 |
2 |
|
2 |
4 |
|
3 |
6 |
Se indico le "marche" posso osservare:
3 pulcini X 2 zampe /pulcini = 6 zampe
ma vale anche il contrario:
2 zampe/pulcini X 3 pulcini = 6 zampe
Se invece si scambiano solo i numeri, si ottiene:
2 pulcini X 3 zampe/ pulcino = ?
Questo problema non può sussistere nella realtà, anche se il risultato formalmente è ancora "6 zampe ".
Questo non succederebbe se prescindessimo dalle marche. Allora:
2 X 3 = 3 X 2 = 6 equivale a contare in modi diversi gli elementi di uno schieramento.
Quindi nei problemi vale la proprietà commutativa ma va precisata e qui l’utilizzo delle marche è importante per avere ben chiaro su cosa si sta operando.
Lo ZERO rappresenta sempre un elemento di difficile introduzione e comprensione.
Le maestre lo introducono spesso come cardinale dell’insieme vuoto:" facciamo il gruppo dei bambini con le scarpe gialle".
Si fa presente la sua importanza nella somma e nella sottrazione:"tolgo una quantità uguale a quella iniziale".
La prof. Longo insiste sull’importanza delle proprietà, alcune possono già essere introdotte in I elementare.
La proprietà distributiva potrebbe ad esempio essere così proposta:
3 X 2 + 3 X 5 = 3 X ( 2 + 5 ) = 3 X 7 = 21
che si giustifica come:
( 3 + 3) + ( 3 + 3 + 3 + 3 + 3 ) = …
La comprensione di un’operazione in colonna può essere stimolata dall’applicazione delle proprietà:
14 X 2 = ( 10 + 4 ) X 2 = 10 X 2 + 4 X 2 = 20 + 8 = 28
Le maestre rilevano la difficoltà di far scrivere questa uguaglianza dai bambini delle prime classi.
La prof. Longo suggerisce di introdurre eventualmente dei simboli, che indichino decine ed unità ad es.
14 = ٱ ׀׀׀׀
14 X 2 = ٱ ׀׀׀׀ + ٱ ׀׀׀׀
Si ribadisce che per far capire le operazioni in colonna si devono capire le proprietà delle operazioni.
Se i bambini in seconda elementare hanno delle difficoltà è meglio rimandare la costruzione delle operazioni in colonna in terza. Per questa via anche le operazioni più complesse diventano semplici.
Es:
405 X 13 ![]()
400 + 5 per 13 volte ![]()
400 + 5 per 10 volte e 400 + 5 per 3 volte
formalmente:
405 X 13 = ( 400 + 5 ) X 13 = ( 400 + 5 ) X 10 + (400 + 5 ) X 3 =
= 400 X 10 + 5 X 10 + 400 X 3 + 5 X 3 = 4000 + 50 + 1200 + 15 = 4050 + 1215 = 5265.
Discorso analogo si può fare per la divisione.
Per concludere il suggerimento è stato di lavorare molto sulla composizione e scomposizione di numeri e sulle proprietà, anche per favorire la memoria visiva e la memorizzazione.
Far capire le cose serve ad abbandonare l'uso acritico degli schemi e a progredire.
Il bambino lavora meglio con la reinvenzione guidata che lo conduce a dare un senso alle attività che gli vengono proposte.
Ci si lascia con il " compito " di leggere
le premesse dei nuovi curricoli.
Riflessioni di una maestra sul terzo incontro.
RICHIESTA: quali sono i contesti che permettono di introdurre la moltiplicazione? Preparare un quadro completo di contenuti da proporre, evidenziando le difficoltà e gli ostacoli che si riscontrano nel processo insegnamento-apprendimento.
Le insegnanti dopo aver premesso che ogni processo di conoscenza deve basarsi sull’accertamento dei prerequisiti, affinché l’acquisizione di ogni concetto sia ben fondata, ritengono opportuno partire sempre da situazioni reali che si presentano quotidianamente per ricercare strategie di soluzione ( problem solving) o dalla curiosità manifestata dagli alunni:
Fatta questa premessa, all’interno del gruppo di lavoro ci si confronta sul percorso seguito per introdurre la moltiplicazione e si scopre che non c’è uniformità nel modo di lavorare , anche se successivamente i diversi metodi di lavoro confluiscono in un contesto comune.
Un gruppo parte da corrispondenze e relazioni ( sempre su situazioni vissute), per passare poi alla registrazione grafica ed alla simbolizzazione tramite tabelle a doppia entrata, fino all’individuazione delle coppie ordinate ottenute, con la presentazione degli schieramenti e l’introduzione della moltiplicazione come numero che rappresenta le coppie formatesi, poi come operatore che sostituisce più addizioni ripetute.
Un altro gruppo invece privilegia un cammino più breve, ritenuto di più semplice acquisizione, che parte invece dalla moltiplicazione come operazione "economica" che può sostituire più addendi uguali.
La docente, dopo questa breve esposizione da parte del gruppo di lavoro, approva la scelta di situazioni reali, ludiche e motorie, anzi ne auspica l’utilizzo per facilitare l’acquisizione di ogni concetto, insiste molto sull’uso della rappresentazione grafica, della manualità, della drammatizzazione , della gestualità, dell’espressione corporea e della successiva verbalizzazione delle esperienze vissute , nel rispetto dei ritmi e dei tempi di apprendimento di ogni bambino. Propone che l’acquisizione di ogni concetto venga sottoposta a verifica e che venga consolidata e ripresa se sussistono lacune, con strategie diverse, in quanto è evidente che l’errore o la difficoltà sono dovuti alla mancata comprensione del concetto.
La docente insiste sulla necessità di partire dai problemi per dare senso e valore ai concetti matematici, in modo particolare per le operazioni di moltiplicazione e divisione è necessario chiedere di inventare procedimenti di risoluzione partendo da rappresentazioni libere per favorire il ragionamento ed evitare dannosi meccanismi.
In questo modo si scopriranno e si stabiliranno dei legami tra i vari concetti che permetteranno un’elasticità e una flessibilità di applicazione evitando la fossilizzazione con schemi precostituiti.
All’obiezione delle insegnanti sul modo di eseguire le moltiplicazioni in colonna , la docente insiste sul fatto che troppo spesso gli insegnanti tendono a facilitare il lavoro degli alunni e a risolvere i problemi al loro posto, mentre la ricerca delle soluzioni deve essere personale e individuale.
Si consiglia di utilizzare le proprietà delle operazioni, la composizione e la scomposizione dei numeri per dare un significato alle operazioni in colonna e per sveltire il calcolo orale cercando strategie che lo facilitino e ne permettano la memorizzazione.
Dassano Antonella