2) La numerazione posizionale.
La base per poter costruire le operazioni in colonna è la rappresentazione posizionale dei numeri naturali. Riflettiamo dunque anzitutto sui passi necessari per giungere a questa rappresentazione.
Il primo passo è porsi il problema di contare un insieme abbastanza numeroso di oggetti:
formare gruppi, contenenti un numero fissato n di oggetti, facilita questo compito. Fissata la base n, una volta ottenuti n gruppi, questi saranno di nuovo raggruppati tra loro per formare un gruppo di gruppi e così via. Nella base 10, si formeranno decine, centinaia, migliaia, ecc.
Si passa in questo modo dal considerare una grande quantità di oggetti, che hanno tutti lo stesso valore, al considerare una quantità molto minore di oggetti, in cui ciascuno di essi ha una suo preciso valore.
A questo punto sono possibili esercizi di passaggio:
dato un numero, formarlo con i raggruppamenti di oggetti;
dato un raggruppamento, individuare il numero corrispondente.
La lettura del numero dipende esclusivamente dagli oggetti che compongono il raggruppamento, indipendentemente dalla posizione di questi oggetti.
Esempio:
![]()
![]()
![]()
![]()
![]()
![]()
da= decina h= centinaio
Qualsiasi sia la disposizione, leggiamo: 1 centinaio, 2 decine, 3 oggetti sciolti (unità) e cioè il numero «centoventitrè».
Il materiale usato può essere vario:
a) non strutturato:
bastoncini, cannucce, stuzzicadenti, avvolti da cordicelle o elastici, magari di vario colore secondo gli ordini di raggruppamento;
bottoni, pasta, con raggruppamenti ottenuti con sacchetti di plastica o scatole;
crocette o pallini, disegnati su un foglio, avvolti da linee di colori diversi per indicare i vari raggruppamenti;
b) strutturato:
materiale multibase (unità, barre, piatti, cubi)
È consigliabile usare materiali di tipo diverso, includendo anche oggetti legati all'esperienza quotidiana dei bambini.
Il secondo passo è la registrazione del numero, che può avvenire prima sull'abaco e poi sul quaderno.
|
Un primo passaggio sull'abaco è disporre casualmente le aste ed indicare unità, decine, centinaia, migliaia, ecc., attraverso il colore o segnando le marche accanto alle aste: |
|
|
Un secondo passaggio è fare a meno del colore o delle marche e decidere un ordine. In questo caso le aste sono allineate, il valore di un anello su ciascuna asta dipende dalla sua posizione nell'allineamento. Questa registrazione è poi trasferita sul quaderno, utilizzando i simboli e le cifre da 1 a 9 per la base 10, oppure da 1 n-1 per una generica base n.
|
|
Si osservi che, fissata la base n, ogni asta dell’abaco può contenere al massimo n-1 anelli: quando si arriva ad aggiungere l’ennesimo anello, si deve cambiare: n anelli su un’asta vengono cambiati con un solo anello nell’asta successiva.
Concludiamo con un brano di G.Vergnaud: "Gli esercizi di passaggio da un materiale o da una rappresentazione ad un'altra possono essere cosi schematizzati (le frecce rappresentano i possibili esercizi di passaggio):
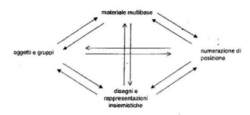
clicca sulla figura per vederla ingrandita
Ecco un esempio in base tre: prendere una piastrella, due barre e una unità, scrivere il numero corrispondente, prendere un numero di fiammiferi corrispondente a quel numero, disegnare la rappresentazione insiemistica corrispondente, mettere questa rappresentazione in rapporto al materiale multibase di partenza.
![]() clicca sulla figura per vederla ingrandita
clicca sulla figura per vederla ingrandita
E' possibile anche far stabilire una corrispondenza biunivoca tra un insieme di oggetti ed un insieme di unità del materiale multibase, far effettuare poi separatamente, ma sempre nella stessa base, da una parte i raggruppamenti degli oggetti in sacchetti, scatole, ecc., e dall'altra i raggruppamenti delle unità in barre, piastrelle, ecc., constatando in seguito la corrispondenza sacchetto - barra, scatola - piastrella. Tutti questi esercizi sono più facili con basi piccole, ma essi devono comunque essere eseguiti anche in base 10. E' anche necessario organizzare , quando il principio della numerazione è stato compreso, un lavoro più approfondito in base dieci. La lettura dei numeri scritti e il dettato di numeri sono esercizi di passaggio da una rappresentazione scritta ad una rappresentazione fonetica e viceversa." (Vergnaud, 1994, p.130)
Osservazioni didattiche.
Sono prerequisiti essenziali l'ordine e la lateralizzazione. Non si deve sottovalutare la
difficoltà insita nell'idea di valore: se si contano 2 centinaia, 3 decine,5 unità, gli oggetti visibili sono 10, ma di tipi diversi e non equivalenti. Ciò può non essere un riconoscimento facile per alcuni bambini. Con essi sarà necessario continuare a ripetere esercizi di conteggio, finchè questa consapevolezza non sia conquistata. punto chiave è comprendere la diversità delle situazioni di contare insiemi poco numerosi oppure insiemi molto numerosi. Non ha molta importanza insistere un lungo tempo sulle decine, poi un lungo tempo sul centinaio, ecc.
Ciò che deve essere compreso è il meccanismo del cambio.
Ci troviamo in pieno accordo con G. Vergnaud, che afferma: "....é soprattutto un modo per far superare il limite aberrante dei numeri a due cifre, che costituisce più un ostacolo che un aiuto alla comprensione del principio fondamentale della numerazione: cioè che una stessa cifra rappresenta un numero n volte più grande, in base n, se è posta nella seconda colonna verso sinistra, piuttosto che se è nella colonna delle unità, n-volte più grande ancora, se è posta nella terza colonna e via di seguito. Il fatto che questo principio si applichi a tutte le traslazioni di una tacca verso sinistra non può essere spiegato se ci si limita ai numeri a due cifre" (G. Vergnaud, 1994)