3) Una caratteristica dello zero

Riprendiamo un caso particolare di raggruppamento, in cui manca un ordine intermedio.

Esempio:

h= centinaio  3 oggetti sciolti ( unità)

Osservando la situazione, riconosciamo senza ambiguità "centotre", ma se vogliamo rappresentare questo numero sul quaderno con la rappresentazione posizionale, abbiamo bisogno di porre questa convenzione: il posto vuoto è riempito da uno zero che toglie ogni ambiguità alla rappresentazione. Infatti:

senza lo zero si avrebbe:

      tredici?       (se non si percepisce il posto vuoto tra le due cifre)

      centotre?   (se si percepisce il posto vuoto)

con lo zero si ha:

     103       centotre, senza nessuna ambiguità di lettura.

Abbiamo così scoperto un nuovo aspetto dello zero, collegato alla rappresentazione posizionale, oltre al primo aspetto di connotare il cardinale di un insieme vuoto.

4) La moltiplicazione per dieci

Conseguenza immediata della rappresentazione posizionale è la moltiplicazione per 10 e viceversa. Questa si estenderà in modo semplice ai decimali, una volta che siano stati introdotti:

7x 10 = 70           70:10 = 7

5x 100 = 500     500:100 = 5

Si presuppone costante riferimento a situazioni che implichino le due operazioni di addizione e sottrazione, una inversa dell'altra (giochi, esercizi in palestra, problemi, griglie, ecc.) Per quanto riguarda la costruzione graduale dell'algoritmo dell'addizione, il primo passo è operare concretamente con oggetti o con l'abaco eseguendo, quando occorre,  il raggruppamento di oggetti, oppure il cambio sull'abaco.

Esempio:  

la somma 25 + 37  sarà così eseguita: dobbiamo contare complessivamente gli oggetti che compongono i raggruppamenti relativi ai due numeri:

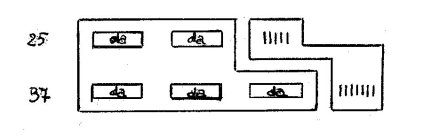
Raggruppiamo le decine e le unità: le decine sono complessivamente 5, le complessivamente 12 ed è necessario operare il cambio, ottenendo ancora (riporto) e due unità sciolte. Il  risultato è quindi 62.

In questo conteggio le proprietà (associativa e commutativa) sono viste "in constatate" ed utilizzate nelle azioni fatte con il materiale.

Il secondo passo è la rappresentazione scritta (sul quaderno, sulla lavagna) di quanto è stato eseguito, lavorando in riga:

25+37= (20+5) + (30+7)=(20+30) + (5+7) =50 + 12 =(50+10) + 2=62

Anche in questo caso, le proprietà sono usate in modo intuitivo, cioè senza preoccuparsi di esprimerle in modo formalizzato.

Il terzo passo, l'operazione in colonna, può essere provocato dall'obiettivo di semplificare la scrittura. Il riporto può essere indicato in vari modi. La rapidità è l'unico effettivo vantaggio rispetto all'operazione in riga, ma deve essere conquistata con passaggi graduali, in modo da non opporsi alla comprensione. Molto interessante è la proposta di Freudenthal (1994, pag.88):

Con la stessa libertà, possiamo inventare con i bambini procedimenti e rappresentazioni per il riporto, finché ci chiederemo come fanno tutti ed accetteremo le convenzioni usuali di scrittura. La possibilità del riporto obbliga a partire dall'unità quando si opera in colonna: infatti le colonne successive all'unità possono venire alterate dal riporto.