Di cosa si tratta

"Teorema in atto" è il nome sintetico, coniato da G. Vergnaud, per indicare un'idea matematica (definizione, proprietà teorema in senso proprio), quando essa è utilizzata in modo implicito come elemento organizzatore di una situazione. Questa può essere un’operazione concreta, un gioco, un problema, ed è vissuta senza che la proprietà matematica sia conosciuta nel suo aspetto formale, definitivo.

Infatti, possiamo parlare di "teorema in atto" solo finché l'idea in questione non viene riconosciuta esplicitamente e formulata con il linguaggio proprio della matematica. A questo punto diventerà una conoscenza matematica vera e propria.

Ouando e' possibile apprendere una nozione incontrandola prima in modo implicito come teorema in atto e raggiungendo poi la proprità matematica attraverso la graduale esplicitazione e traduzione nel linguaggio proprio della disciplina, questo appare una via regia per l'apprendimento, poiché in grado di produrre conoscenze stabili e significative. In questo caso, infatti, la conoscenza matematica affonda le radici nell'esperienza, e la strada è quella auspicata concordemente dagli esperti di scienza cognitiva.

Facciamo alcuni esempi di teoremi in atto, per comprendere meglio cosa siano e come possano essere utilizzati nell'insegnamento della matematica.

Esempio 1

Nel procedimento del contare gli elementi di un insieme sono contenute forti idee matematiche implicite, e cioè quelle di relazione d'ordine, di corrispondenza biunivoca e di cardinale. Vergnaud illustra come l'esistenza, o la non esistenza, del concetto implicito di cardinale si può inferire dal comportamento dei bambini.

"Quando conta un insieme di sei elementi, la maggior parte dei bambini di 5 o 6 anni conta: uno, due, tre, quattro, cinque, sei ... sei! Non solo essi devono stabilire una corrispondenza biunivoca tra gli oggetti da contare, i gesti delle dita, i movimenti degli occhi e le parole-numero, ma sentono anche la necessità di dire la parola "sei" due volte. La prima espressione si riferisce al sesto elemento dell'insieme, la seconda si riferisce al cardinale dell'insieme:

questa doppia espressione significa che il concetto di cardinale è stato ben riconosciuto.

I bambini più grandi non ripetono "sei", ma lo pronunciano solo con più enfasi rispetto agli altri numeri. Ma ci sono bambini che non ripetono "sei" e quando gli si chiede quanti oggetti ci sono, non sono capaci di rispondere e cominciano di nuovo a contare. Per i bambini che sanno cardinalizzare, "sei" riassume le informazioni sull'insieme sottoposto alla procedura del contare. Non è così per i bambini che non sanno cardinalizzare. Quindi si può inferire l'esistenza o la non esistenza del concetto di cardinale dal comportamento dei bambini." (Vergnaud, 1992, p. 146)

Esempio 2

"È ora ben noto che se devono contare un insieme di bambini, dopo aver già contato separatamente 4 maschi e 3 femmine, molti bambini di 5 o 6 anni contano di nuovo l'intero insieme. E un grande progresso essere capaci di dire 4+3 = 7 o anche di partire da 4 e poi contare 3 passi avanti. Questo abbrevia la procedura del contare tutto l'insieme. Questa scoperta (è proprio una scoperta per gli studenti, perché normalmente nessun maestro la insegna ai bambini) può essere considerata come il riconoscimento spontaneo dell'assioma fondamentale della teoria della misura:

card( AUB)= card A+card B

purché A e B abbiano intersezione vuota. Non si conta di nuovo tutto l'insieme; basta sommare i cardinali dei due sottoinsiemi. "' (Vergnaud, 1992, pag. 147)

Si può riconoscere facilmente che la stessa proprietà viene utilizzata in modo implicito ogni volta che un bambino esegue correttamente un problema in cui si debbono sommare due misure dello stesso tipo, due prezzi, due pesi, due aree, ecc.

Di seguito l'autore fa vedere come anche la commutatività della somma si può riconoscere "in atto". Ma più interessante è un altro esempio, che riguarda una nozione meno elementare, la linearità di una funzione.

 

 

Esempio 3

"In un problema orale alcuni studenti dovevano calcolare la quantità di zucchero necessaria per 5O bambini che andavano in colonia per 28 giorni. Si sapeva che la quantità occorrente per 10 bambini, per una settima era 3,5 kg. Alcuni studenti dissero che 50 bambini è 5 volte più di 10, e 28 giorni è 4 volte più lungo di una settimana; perciò il consumo di zucchero doveva essere 20 volte più grande. Il non banale teorema in atto rilevato in questa procedura può essere scritto:

Consumo (5x10, 4x7) = 5x4x Consumo (10, 7)

che è un caso particolare della funzione bilineare:

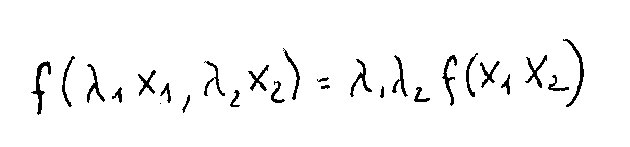
Naturalmente i facili valori numerici rendono possibile a ragazzi di 11 anni estrarre i rapporti 5 e 4; e non c'è per loro alcuna difficoltà concettuale nel riconoscere la doppia proporzionalità del consumo rispetto al numero di persone ed alla durata del tempo. Perciò c'è un grosso divario tra il teorema in atto da essi usato ed il teorema generale. Ma, di nuovo, l'idea matematica è presente." (Vergnaud, 1992, pag. I 48)

Conseguenze teoriche

Esse sono state tutte esplicitate da G. Vergnaud nelle sue opere.

* Nell'apprendere, un concetto non viene mai affrontato da solo, ma insieme agli altri che più naturalmente sono ad esso collegati, e che possiamo raggruppare in un "campo concettuale". Ad esempio addizione e sottrazione, insieme alle loro proprietà, formano un unico campo concettuale, moltiplicazione e divisione formano un altro campo concettuale. Situazioni e problemi non riguardano mai una sola nozione, ma un intero campo concettuale, poiché è quasi impossibile pensare ad un problema che contenga un solo particolare della struttura concettuale, senza coinvolgerne altri.

I problemi che riguardano la struttura additiva e quella moltiplicativa sono classificati da G Vergnaud in (Vergnaud, 1994).

* Ogni apprendimento matematico significativo è un apprendimento a lunga scadenza.

* Un concetto matematico, dal punto di vista genetico, cioè dal punto di vista di un soggetto che apprende, non si identifica con la sua espressione formale, contenuta nell'esposizione matematica di un trattato. Esso è costituito da una terna di insiemi:

- l'insieme delle situazioni che rendono il concetto significativo in una varietà di aspetti;

- l'insieme degli invarianti operazionali (proprietà, relazioni, oggetti, teoremi in atto che sono progressivamente afferrati dagli studenti)

l'insieme dei simboli linguistici e non linguistici che rappresentano quegli invarianti e che sono usati per indicarli, per comunicare e discutere sudi essi.